統計:線性迴歸Linear Regression之適用範圍與SPSS操作
線性迴歸(Linear Regression)主要用來分析一個或多個自變數與一個依變數之間的線性關係,以及依變數的未來趨勢。簡單來說,就是當我們想了解某些因素如何影響某個結果時,線性迴歸可以幫助我們找到這些因素和結果之間的關聯強度與方向。具體來說皮爾森相關係數和線性迴歸都可以用來探討變數之間的關聯性,但線性迴歸的重點在於預測和量化這些關係,而不單純是衡量它們之間的強度。
線性迴歸的適用情境
預測汽車油耗:根據車輛的車重、引擎排量和駕駛習慣,預測汽車的油耗(每公升行駛的距離)。
預測房屋價格:根據房屋的面積、建造年份和所在區域,預測房屋的市場價格。
預測運動員的比賽成績:根據運動員的訓練時間、體重和年齡,預測運動員在比賽中的成績。
預測銷售額:根據廣告支出、季節因素和促銷活動的時間長度,預測某產品的月銷售額。
預測健康指數:根據年齡、運動頻率和飲食習慣,預測一個人的健康指數(如心臟病風險、血糖水平等)。
SPSS操作範例
根據學生的平時作業分數、出席率和學習時間,預測學生的期末考試成績。作業分數、出席率、學習時間可能與期末成績呈現線性關係,線性迴歸可以幫助學校預測學生的最終學業表現。
Step 1. 在SPSS變數視圖中,預先定義資料欄位。
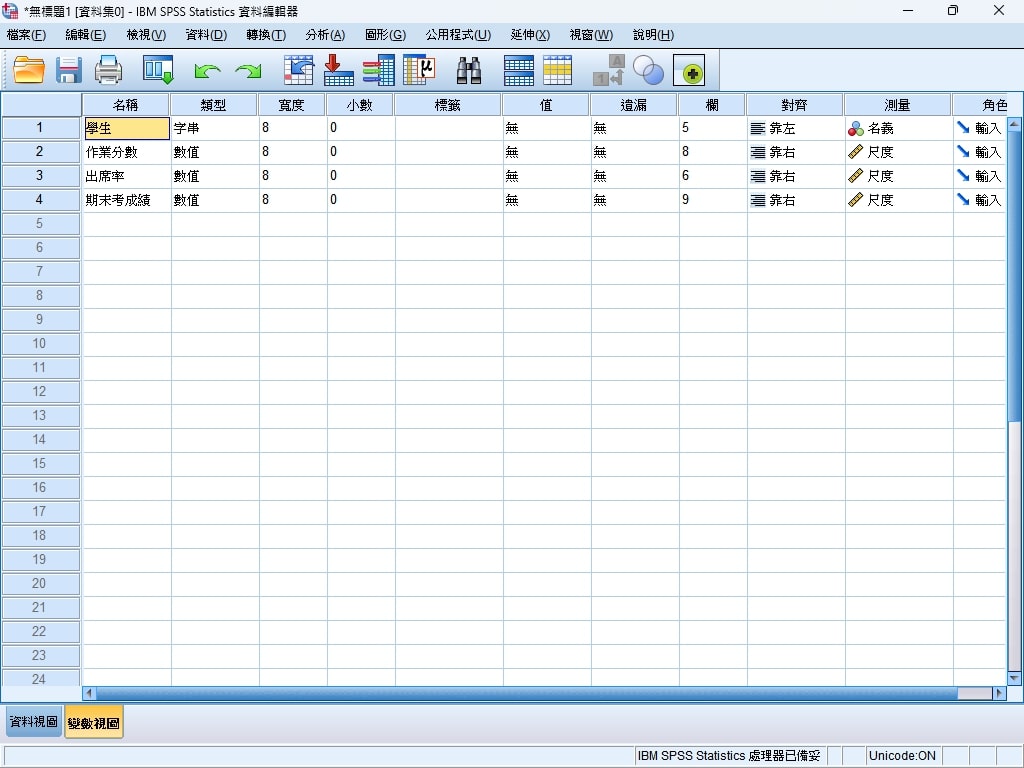
Step 2. 將收集到的數據,複製到SPSS資料視圖內。
學生 作業分數 出席率% 期末考成績
1 85 90 88
2 78 85 82
3 92 95 94
4 80 70 75
5 60 50 65
6 95 98 96
7 76 80 78
8 88 92 90
9 72 65 70
10 84 87 85
11 90 91 92
12 68 60 72
13 77 85 80
14 65 55 67
15 93 97 95
16 82 88 83
17 70 65 68
18 79 75 80
19 85 90 87
20 75 70 74
21 91 93 93
22 67 60 69
23 89 90 91
24 74 78 76
25 98 99 99
26 82 85 84
27 81 86 83
28 73 72 75
29 96 97 98
30 79 80 80
Step 3. 點選分析>迴歸>線性。
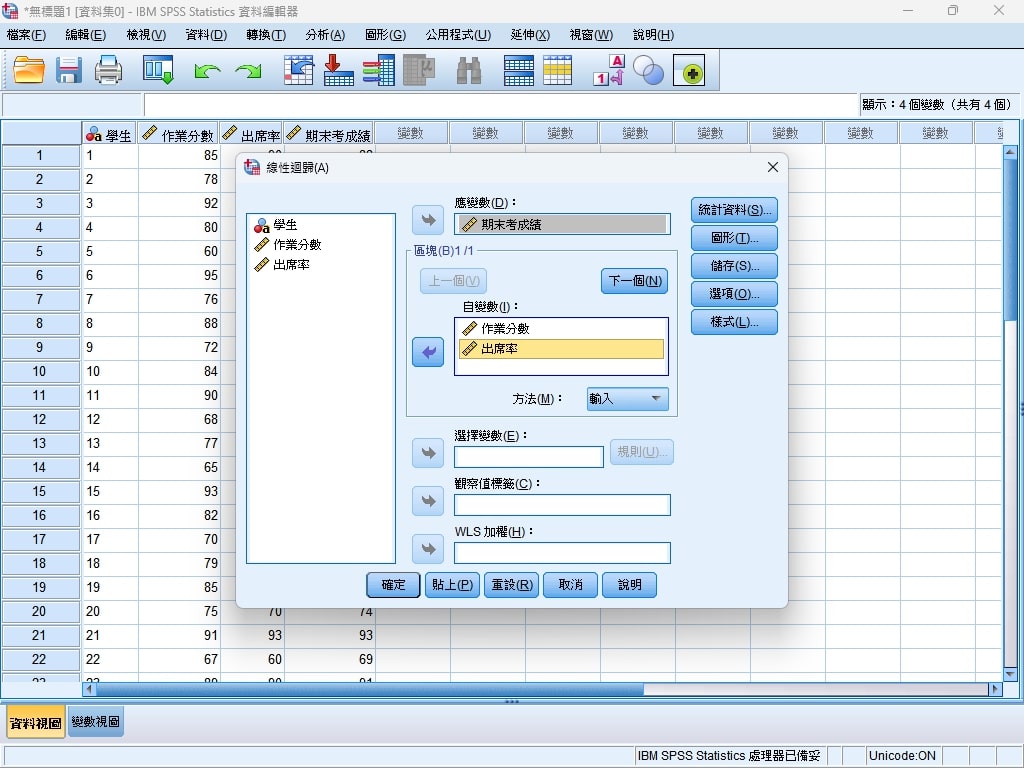
Step 4. 將作業分數與出席率放入自變數欄位,期末考成績放入應變數欄位。
Step 6. 最後SPSS就會將統計分析後的數據報告呈現給我們看了。
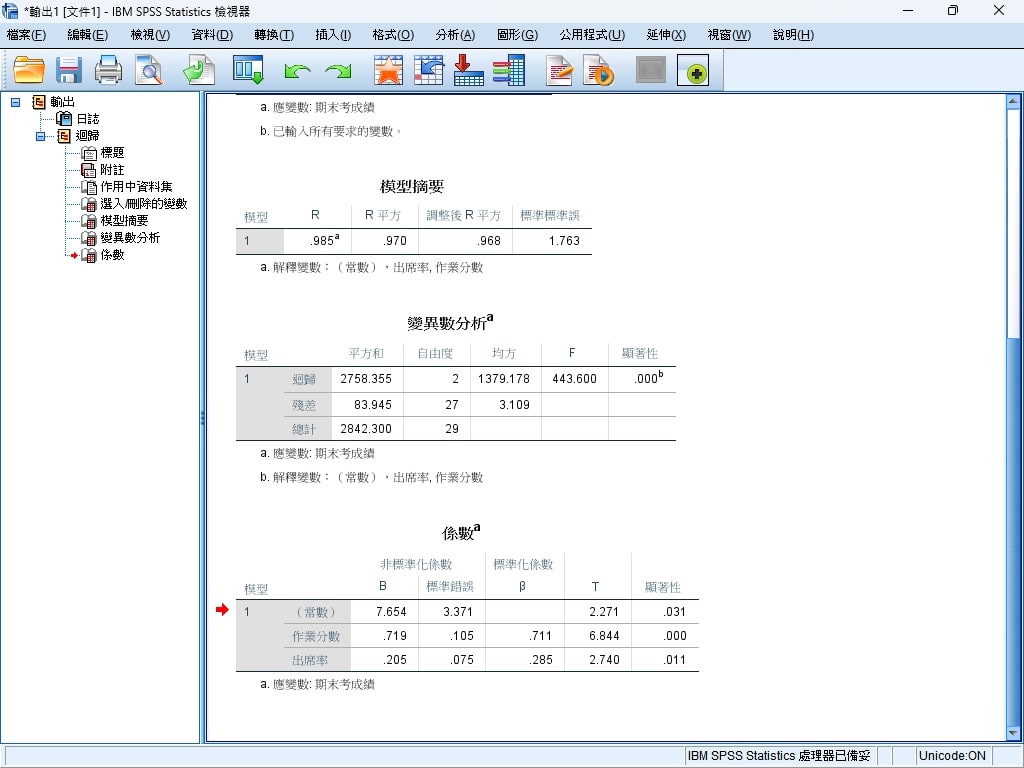
分析報告
以上面的例子,我們的獲取的分析報告資訊大致上如下:
本研究旨在分析「作業分數」和「出席率」兩個變數對「期末考成績」的預測能力。
- 模型摘要
根據線性迴歸分析的結果,模型的R值為0.985,表示期末考成績與作業分數和出席率之間具有非常強的正相關關係。R平方值為0.970,表示該迴歸模型可以解釋97%的期末考成績變異,顯示該模型具有極高的解釋力。調整後的R平方值為0.968,考慮到模型中自變量數量後,仍然保持良好的解釋能力。
- 變異數分析
變異數分析(ANOVA)結果顯示,迴歸模型的F值為443.600,且其顯著性水準p=0.000遠小於0.05,表明模型整體顯著,即作業分數和出席率對期末考成績有顯著的預測作用。
- 係數分析
迴歸方程式為:(我們可以從這個公式推論未來的期末成績)
期末考成績 = 7.654 + (0.719 * 作業分數) + (0.205 * 出席率)
常數項(截距)為 7.654,表示當作業分數和出席率均為零時,期末考成績的預測值為 7.654。
作業分數的迴歸係數為0.719,標準誤為0.105。這表示每增加1分的作業分數,期末考成績將平均增加0.719分。該係數的t值為6.844,顯示其顯著性(p = 0.000),因此作業分數對期末考成績具有顯著影響。
出席率的迴歸係數為0.205,標準誤為 0.075,表示每增加1%的出席率,期末考成績將平均增加0.205分。該係數的t值為2.740,顯示其顯著性(p = 0.011),表明出席率對期末考成績也有顯著影響,雖然相對於作業分數的影響較小。
⭐結論
作業分數和出席率均對期末考成績有顯著的正向預測作用,由於模型解釋了97%的期末考成績變異,顯示這些變數是期末考成績的有效預測因子。這表明學生的作業表現與出席情況對最終的學期成績有顯著的影響。
相關連結:
- 統計:常態分佈、平均值、變異數與標準差
- 統計:一個簡單的樣本變異係數的運算範例
- 統計:一個簡單的幾何平均數的運算範例
- 統計:比較平均數法、T檢定、F檢定、p顯著性之說明
- 統計:獨立樣本T檢定之適用範圍與SPSS操作
- 統計:成對樣本T檢定之適用範圍與SPSS操作
- 統計:單因子變異數分析One-Way ANOVA之適用範圍與SPSS操作
- 統計:多因子變異數分析Two-Way ANOVA之適用範圍與SPSS操作
- 統計:皮爾森相關係數Pearson Correlation之適用範圍與SPSS操作
- 統計:線性迴歸Linear Regression之適用範圍與SPSS操作