統計:皮爾森相關係數Pearson Correlation之適用範圍與SPSS操作
皮爾森相關係數(Pearson Correlation)適用於測量兩個連續變數之間的線性關聯性,它可以幫助我們了解這兩個變數之間的關聯強度和方向。簡單來說,就是用來判斷兩個變數之間是否存在某種程度的相互關聯,並且這種關聯是正向還是負向?
皮爾森相關係數之線性關係區分強度(範圍在-1到+1之間),當相關係數接近1時表示兩者有強烈的正相關、接近-1時表示兩者有強烈的負相關、接近0則表示兩者之間沒有線性關聯。
皮爾森相關係數的適用情境
研究某減重計畫的運動時間與體重變化之間是否存在正向相關,即運動時間越長,體重變化越顯著。
研究學生的學習時間與成績之間是否存在正相關,即學習時間越長,學習成效越好。
研究某款手機應用程式使用頻率與用戶滿意度之間的關聯,是否存在正向或負向的相關性。
研究員工的工時長度與工作滿意度之間的關係,是否存在負相關,即工時越長,員工滿意度是否會降低。
研究兩種教育方法的使用率與學生的學習成效之間的關聯,是否存在顯著的線性關聯。
SPSS操作範例
某學校主張開設證照輔導班,就可以有效提升學生的證照數量,故我們想要得知證照輔導班與證照數量之間是否存在顯著的線性關聯?
Step 1. 在SPSS變數視圖中,預先定義資料欄位。
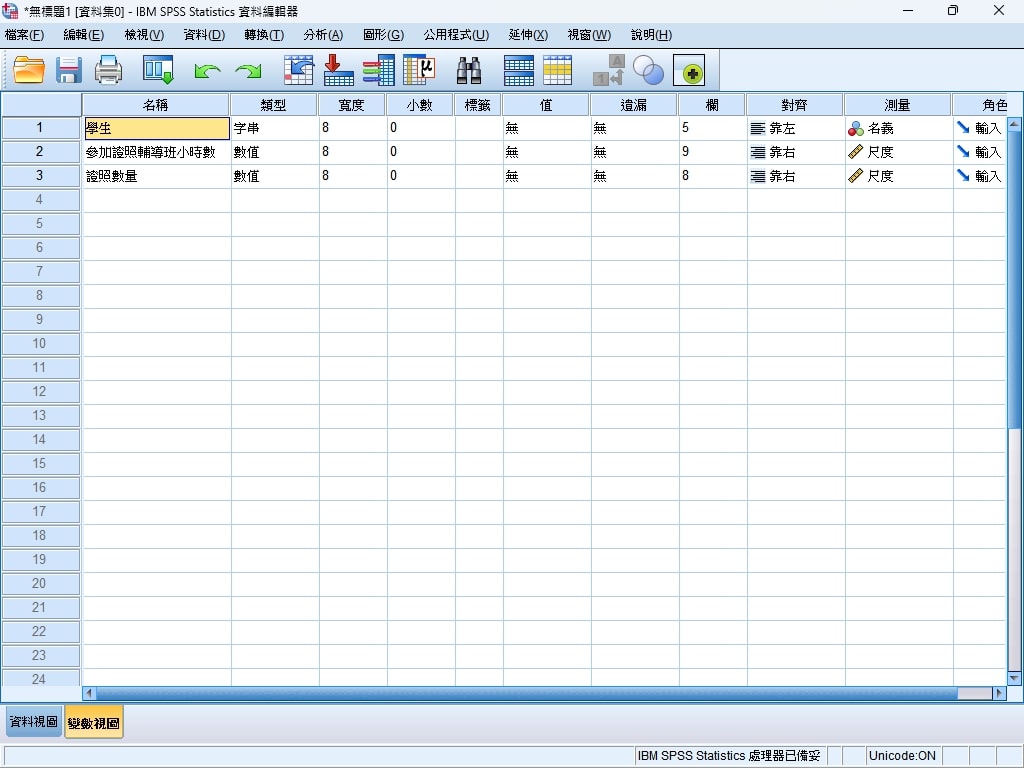
Step 2. 將收集到的數據,複製到SPSS資料視圖內。
學生 參加證照輔導班小時數 證照數量
1 5 3
2 7 4
3 3 2
4 8 5
5 10 6
6 5 4
7 12 7
8 6 6
9 15 8
10 9 5
11 4 3
12 6 5
13 2 2
14 8 6
15 1 8
16 5 3
17 7 5
18 9 7
19 1 9
20 1 10
21 6 4
22 8 5
23 1 7
24 1 8
25 1 7
26 9 6
27 1 8
28 1 9
29 7 5
30 5 3
Step 3. 點選分析>相關>雙變異數。
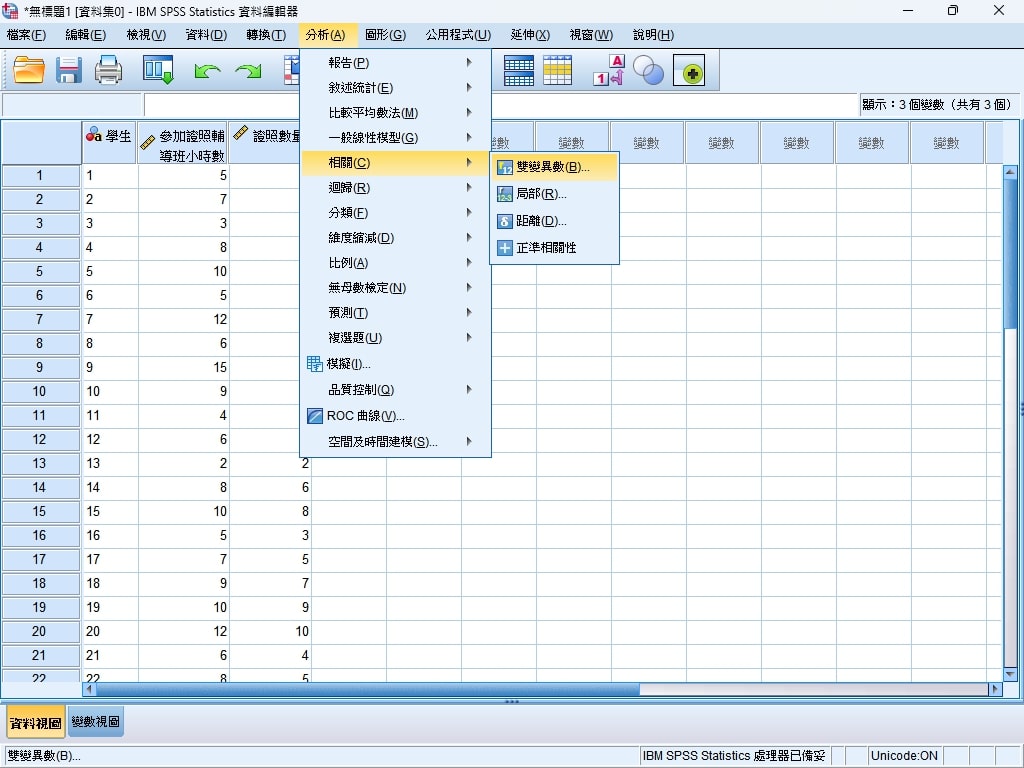
Step 4. 將參加證照輔導班小時數與證照數量放入變數欄位,並勾選Pearson(皮爾森相關係數)。
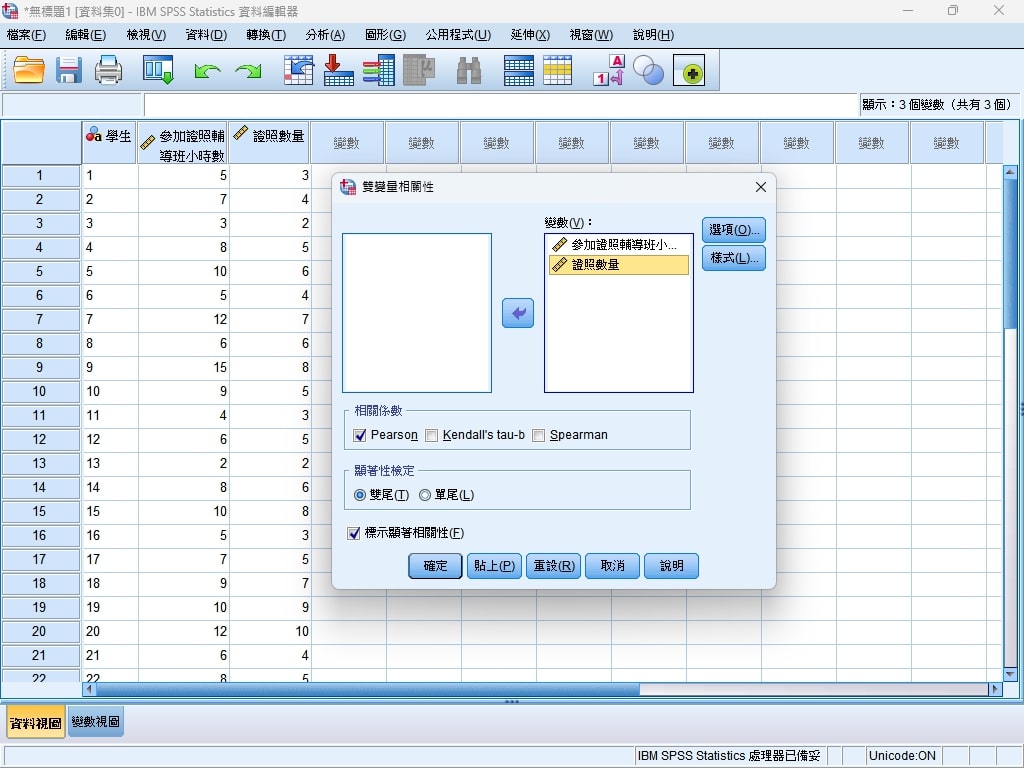
Step 6. 最後SPSS就會將統計分析後的數據報告呈現給我們看了。
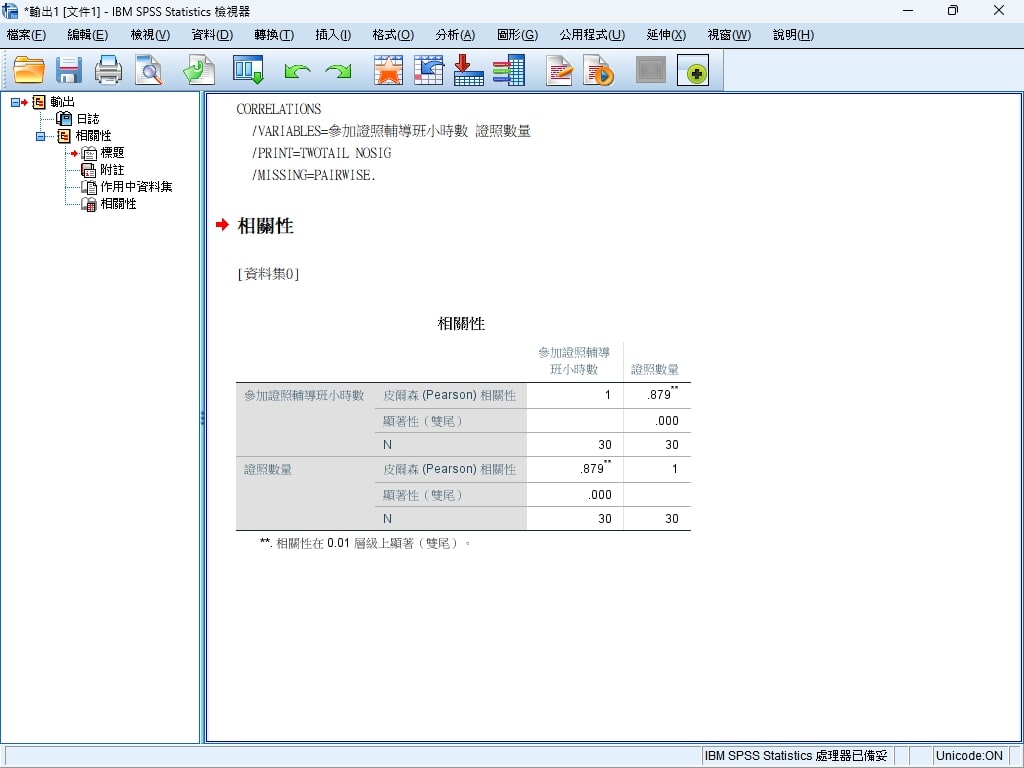
分析報告
以上面的例子,我們的獲取的分析報告資訊大致上如下:
皮爾森相關係數(Pearson Correlation):
參加證照輔導班小時數與證照數量之間的皮爾森相關係數為0.879,這是一個強烈且正向的相關性。
這意味著,隨著學生參與證照輔導班的時間增加,他們所獲得的證照數量也顯著增加。兩者之間呈現出明顯的正相關。
顯著性(Significance):
- 顯著性值(p值)為0.000,小於0.01,這表示兩者之間的相關性在0.01水準上是顯著的。換句話說,可以推斷出,證照輔導班的參與時間與證照數量之間的關聯並非由隨機機會所導致,而是具有統計學上的顯著意義。
⭐結論
學生參與證照輔導班的時間與他們獲得的證照數量之間存在強烈的正相關,這項相關性具有顯著性,因此可以合理推論,學生參與證照輔導班的時間越長,他們獲得的證照數量越多。
相關連結:
- 統計:常態分佈、平均值、變異數與標準差
- 統計:一個簡單的樣本變異係數的運算範例
- 統計:一個簡單的幾何平均數的運算範例
- 統計:比較平均數法、T檢定、F檢定、p顯著性之說明
- 統計:獨立樣本T檢定之適用範圍與SPSS操作
- 統計:成對樣本T檢定之適用範圍與SPSS操作
- 統計:單因子變異數分析One-Way ANOVA之適用範圍與SPSS操作
- 統計:多因子變異數分析Two-Way ANOVA之適用範圍與SPSS操作
- 統計:皮爾森相關係數Pearson Correlation之適用範圍與SPSS操作
- 統計:線性迴歸Linear Regression之適用範圍與SPSS操作