統計:多因子變異數分析Two-Way ANOVA之適用範圍與SPSS操作
多因子變異數分析(Two-Way ANOVA)適用於同時比較兩個或更多因子對於結果變數的影響,並評估不同因子之間是否存在交互作用。換句話說,是用來檢驗多組、多種或多層次的分類中,是否各自和彼此之間的差異具顯著性。
多因子變異數分析Two-Way ANOVA的適用情境
某減重計畫,在不同的飲食控制(低碳飲食、低脂飲食)與不同運動強度(低、中、高強度)的組合下,對體重變化是否有顯著差異,且是否存在飲食和運動強度的交互作用。
某教學方法,在不同性別(男性、女性)與不同年級(低、中、高年級)的學生中,學習成效是否有顯著差異,並且性別和年級間是否存在交互作用。
某紓壓App,在不同焦慮程度(輕度、中度、重度)與不同使用頻率(每天使用、每週使用)下,對焦慮指數的影響是否顯著,並且焦慮程度與使用頻率間是否存在交互作用。
彈性工時制度,在不同的班別(早班、午班、晚班)與不同職位(管理層、非管理層)之間,對工作滿意度是否有顯著差異,並且班別與職位之間是否存在交互作用。
使用某款空氣清淨機,在不同空間(客廳、臥室、書房)與不同使用時間(早上、下午、晚上)的組合下,對空氣品質的影響是否顯著,並且空間與使用時間之間是否存在交互作用。
SPSS操作範例
某學校宣稱OO措施可以有效平衡各學院之男女性別學生的證照數量,故我們想要得知這個OO措施是否真如宣稱般的具備顯著效果?
Step 1. 在SPSS變數視圖中,預先定義資料欄位。其中可以去指定值欄位,讓後續報告中令人困惑的代表值可以透過標籤來還原與表明。
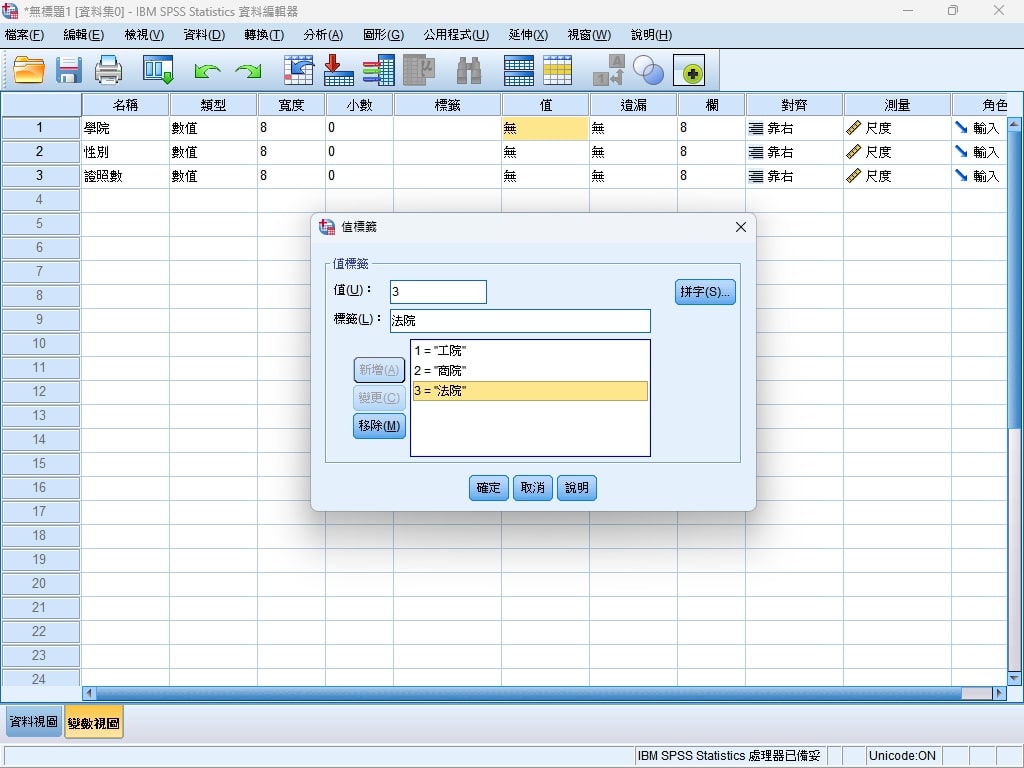
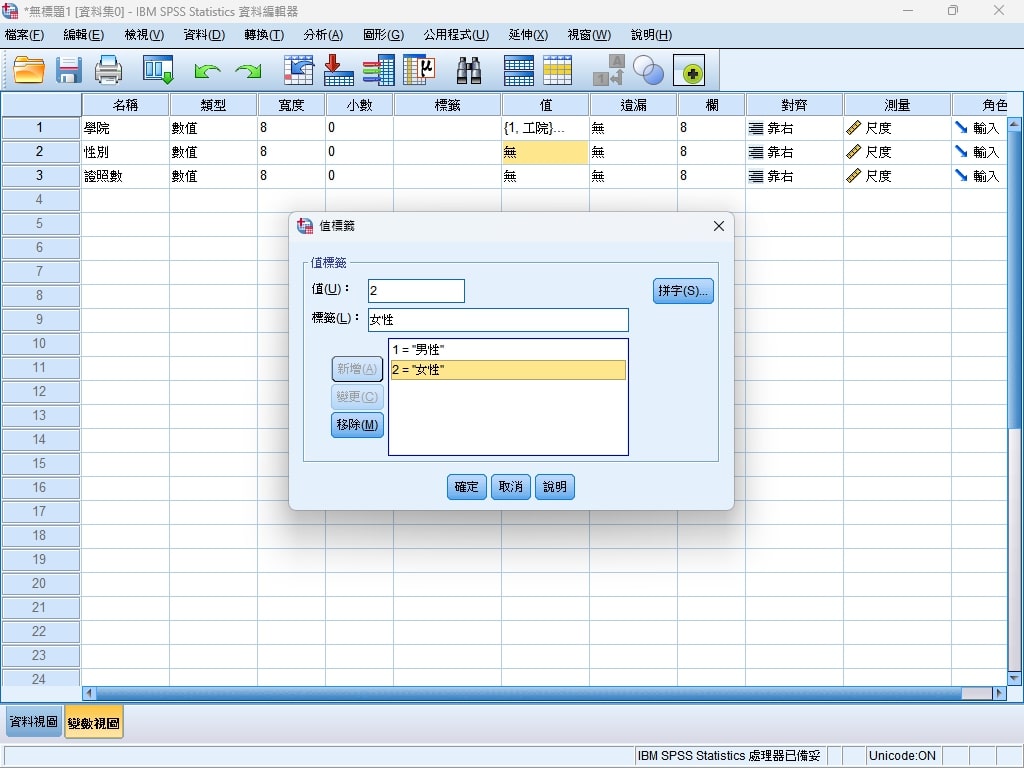
Step 2. 將收集到的數據,複製到SPSS資料視圖內,請預先將學院取代成數值、性別取代成數值。(亦可進入SPSS中進行取代,但實在是太麻煩了,勸你在外部的資料編輯環境中做會簡單很多)
學院 性別 證照數
1 1 15
1 1 17
1 1 14
1 2 12
1 2 10
1 2 13
2 1 8
2 1 9
2 1 7
2 2 11
2 2 10
2 2 12
3 1 6
3 1 5
3 1 7
3 2 9
3 2 8
3 2 10
Step 3. 點選分析>一般線性模型>單變異數。
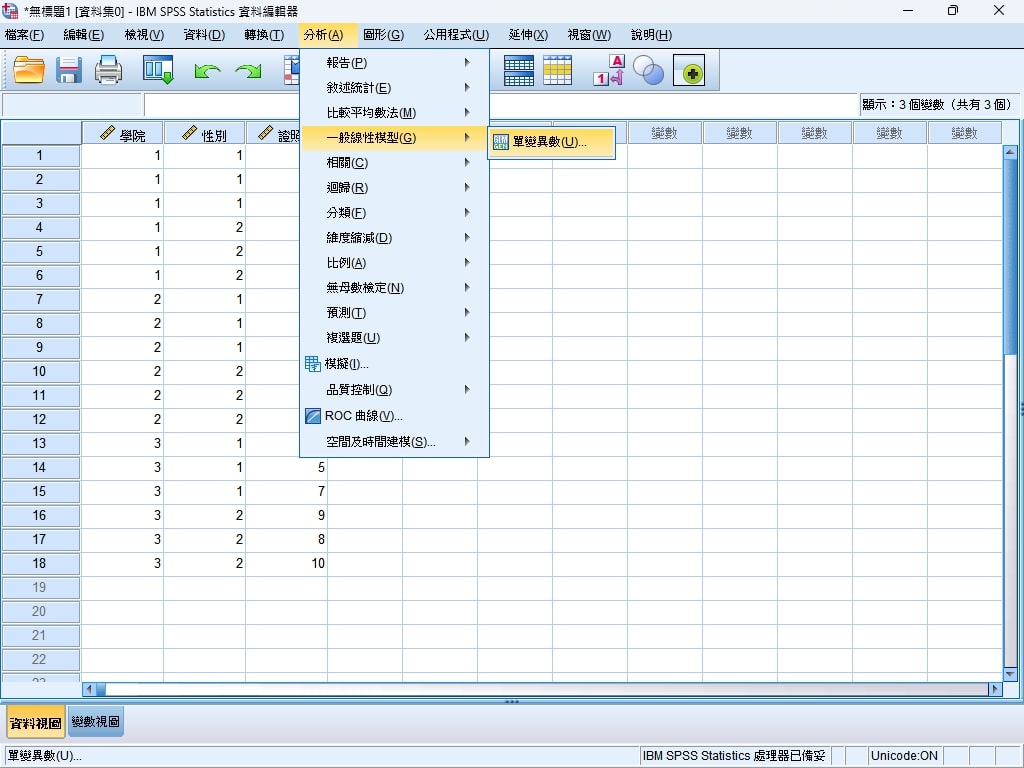
Step 4. 將證照數放入應變數欄位(依變數;Dependent Variable),學院與性別放入固定因子欄位(Fixed Factor)。
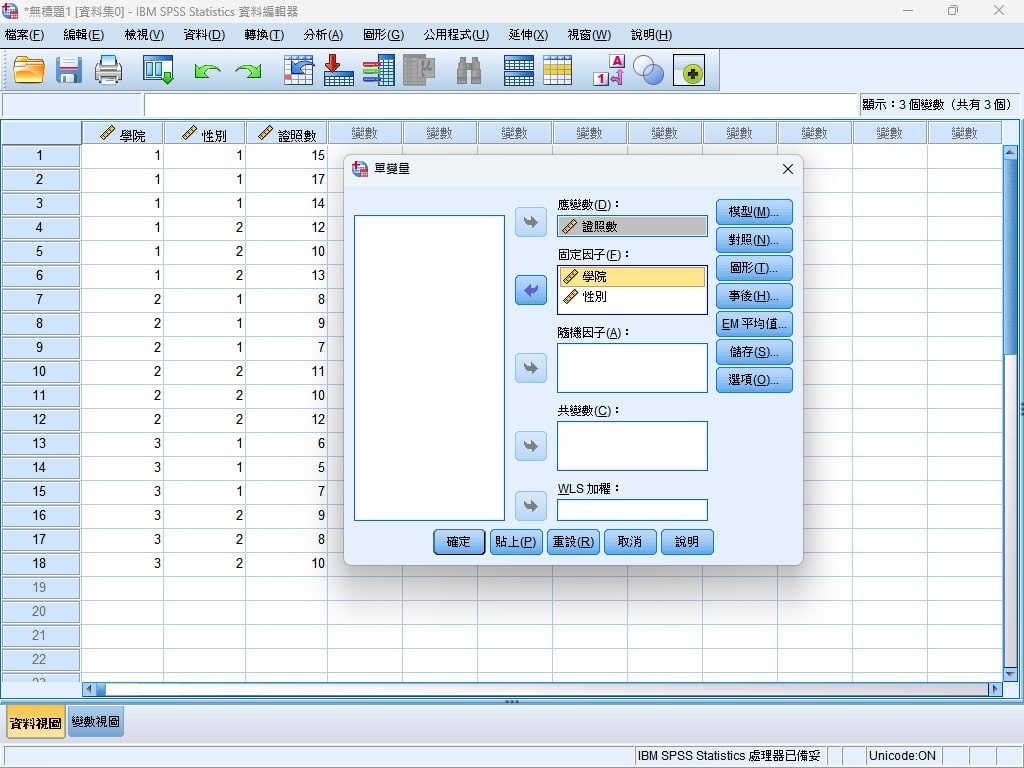
Step 5. 點選事後,將因子學院放入此項目的事後檢定欄位,並勾選Tukey、Scheffe(作為回收樣本數量不同之校正)。
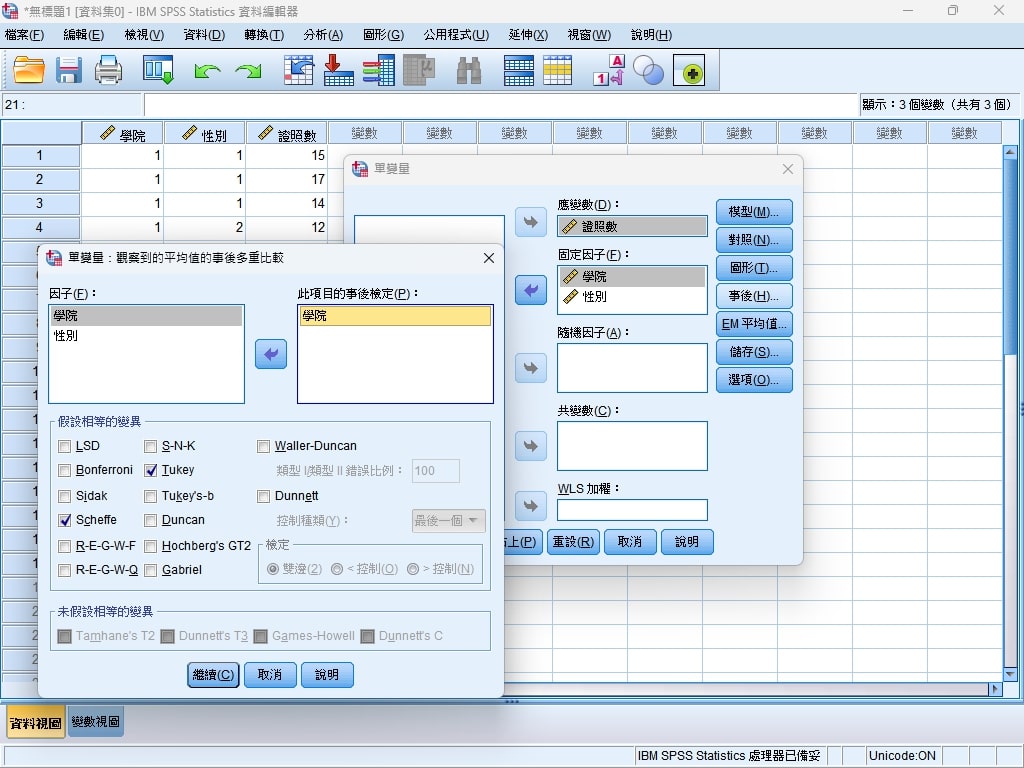
Step 6. 最後SPSS就會將統計分析後的數據報告呈現給我們看了。
分析報告
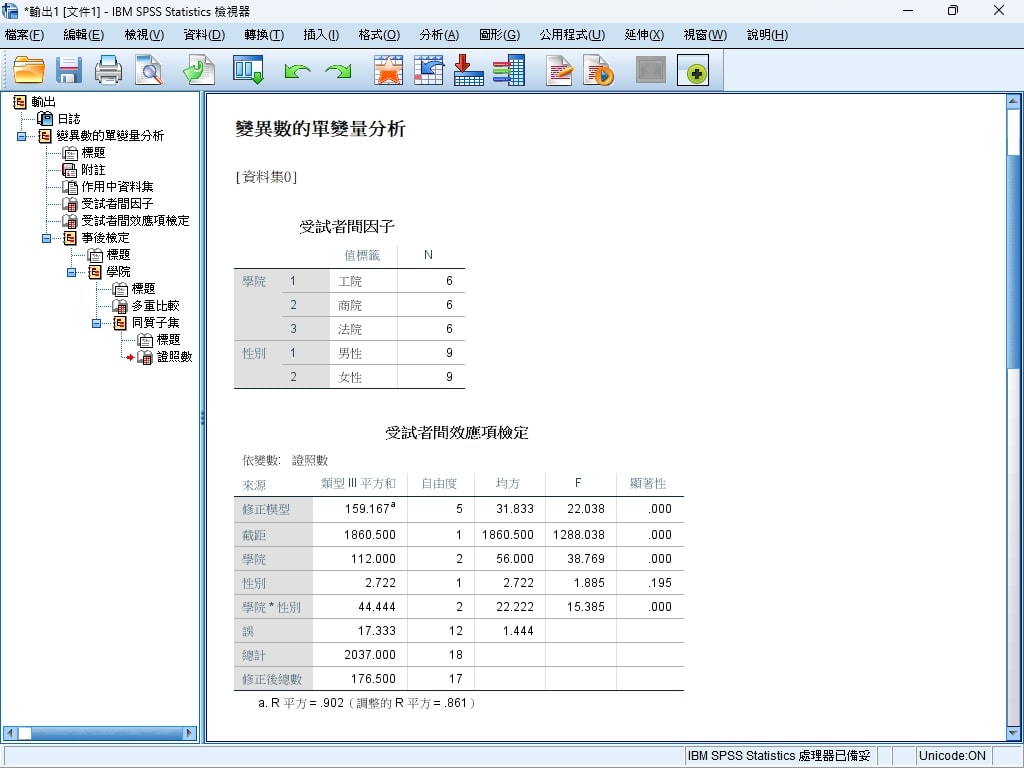
以上面的例子,我們的獲取的分析報告資訊大致上如下:
主效果分析
- 學院的主效果
學院的主效果在證照數上具有顯著差異(F(2,12)=38.769, p=.000)。這表示在不同學院之間,學生持有的證照數量存在顯著差異。
- 性別的主效果
性別的主效果不顯著(F(1,12)=1.885, p=.195)。這表示在男性與女性之間,證照數量沒有顯著差異。
交互作用分析
- 學院 * 性別的交互作用
學院與性別之間的交互作用顯著(F(2,12)=15.385, p=.000),表示學院與性別共同影響證照數量,顯示不同學院的男性與女性在持有證照數上存在顯著差異。
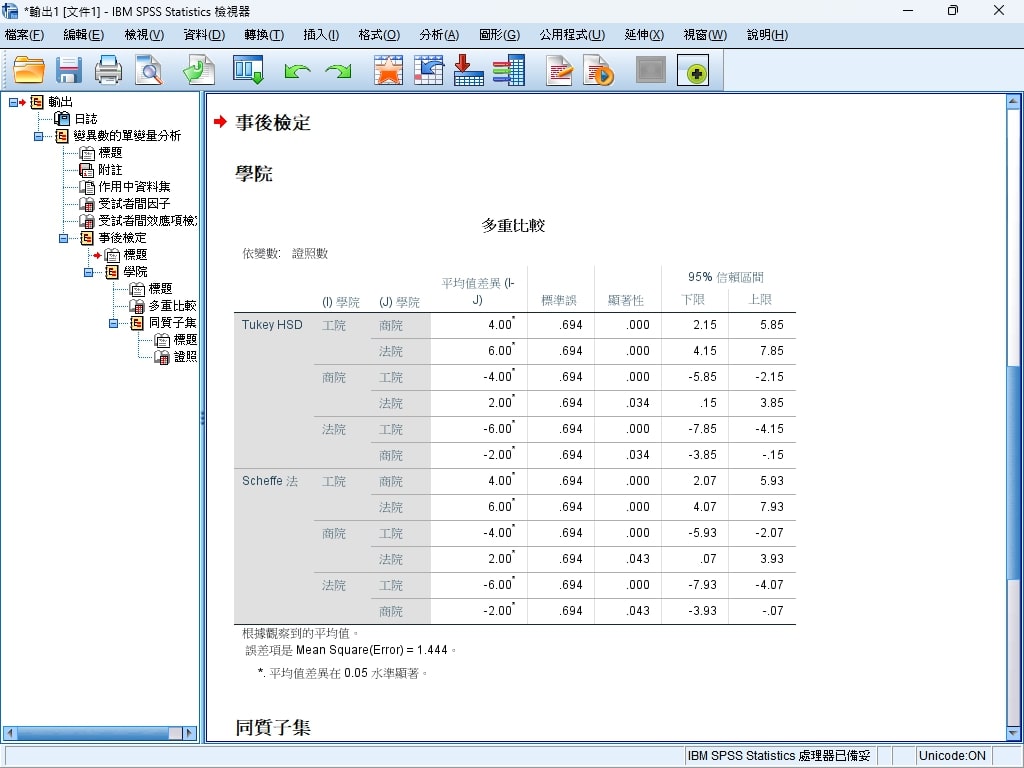
- 事後檢定(Post Hoc Tests)
使用Tukey HSD與Scheffe法的結果一致,發現:
- 工院與商院之間的平均證照數量差異顯著(p=.000),工院學生的平均證照數量顯著高於商院。
- 工院與法院之間的平均證照數量差異顯著(p=.000),工院學生的平均證照數量顯著高於法院。
- 商院與法院之間的平均證照數量差異也顯著(p=.034),商院學生的平均證照數量高於法院。
⭐結論
本研究結果將顯示OO措施對於平衡各院、各性別之學生證照數量的影響:
- 各學院之間的證照數量存在顯著差異,因此「未達到在學院層級平衡證照數量的目標」。
- 各性別之間的證照數量不存在顯著差異,因此「達到在性別層級平衡證照數量的目標」。
- 發現:學院與性別之間存在顯著的交互作用。工院學生的證照數量顯著高於其他學院,顯示該措施對不同學院的效果有所差異。
相關連結:
- 統計:常態分佈、平均值、變異數與標準差
- 統計:一個簡單的樣本變異係數的運算範例
- 統計:一個簡單的幾何平均數的運算範例
- 統計:比較平均數法、T檢定、F檢定、p顯著性之說明
- 統計:獨立樣本T檢定之適用範圍與SPSS操作
- 統計:成對樣本T檢定之適用範圍與SPSS操作
- 統計:單因子變異數分析One-Way ANOVA之適用範圍與SPSS操作
- 統計:多因子變異數分析Two-Way ANOVA之適用範圍與SPSS操作
- 統計:皮爾森相關係數Pearson Correlation之適用範圍與SPSS操作
- 統計:線性迴歸Linear Regression之適用範圍與SPSS操作