統計：成對樣本T檢定之適用範圍與SPSS操作

成對樣本T檢定適用於比較同一組樣本在兩個不同情境下的平均數之間是否有顯著差異。簡單的說，就是量測前後情境、干預前後，針對同一群體在不同情境下的表現是否存在顯著的變化。

成對樣本T檢定的適用情境

• 某種運動訓練前後，青年組的體能表現是否有顯著改善。

• 飲食控制方案介入前後，參與者的體重是否有顯著變化。

• 語言學習APP使用前後，使用者的英語詞彙量是否有顯著增加。

• 培訓課程參加前後，員工對新技術的掌握程度是否有顯著提高。

• 輔助睡眠方案實行前後，參與者的睡眠質量是否有顯著改善。

SPSS操作範例

某校宣稱ＯＯ教學方法可以有效提升學生微積分成績，因此我們先在施行ＯＯ教學方法前先測試取得一次學生前測成績，並於施行後再度取得一次學生後測成績，藉以觀察對於微積分成績是否有顯著提升？

Step 1. 在SPSS變數視圖中，預先定義資料欄位。

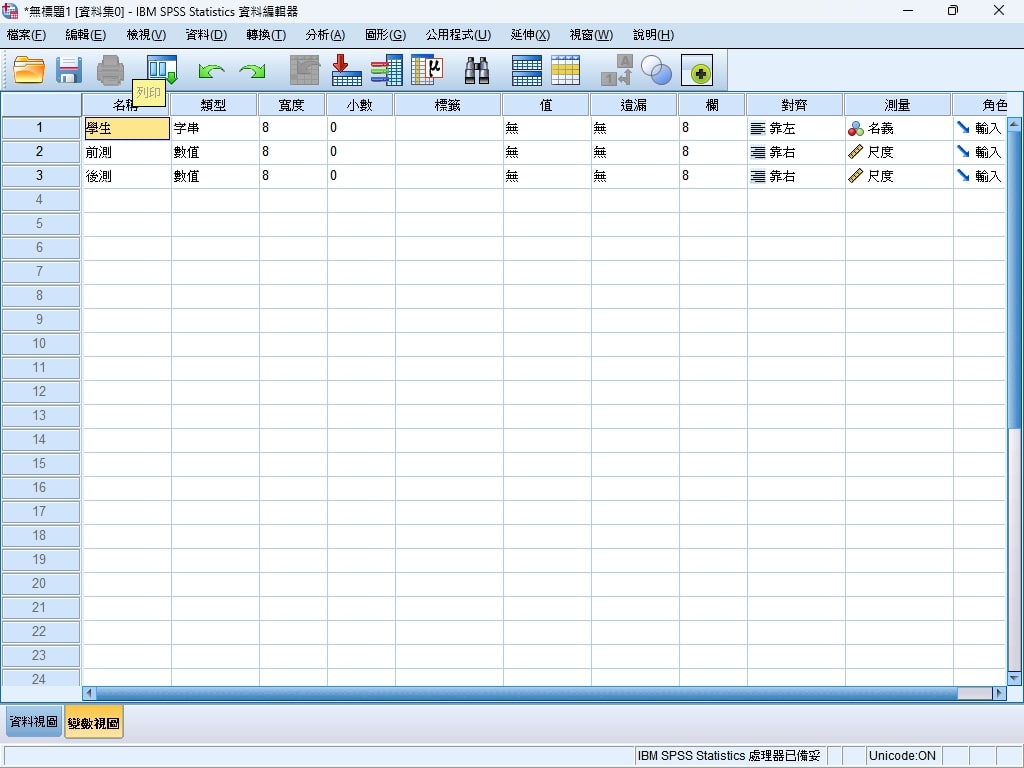
Step 2. 將收集到的數據，複製到SPSS資料視圖內。

學生 前測 後測
A    65   72
B    70   78
C    62   68
D    80   85
E    75   83
F    68   74
G    72   79
H    77   84

Step 3. 點選分析＞比較平均數法＞成對樣本T檢定。

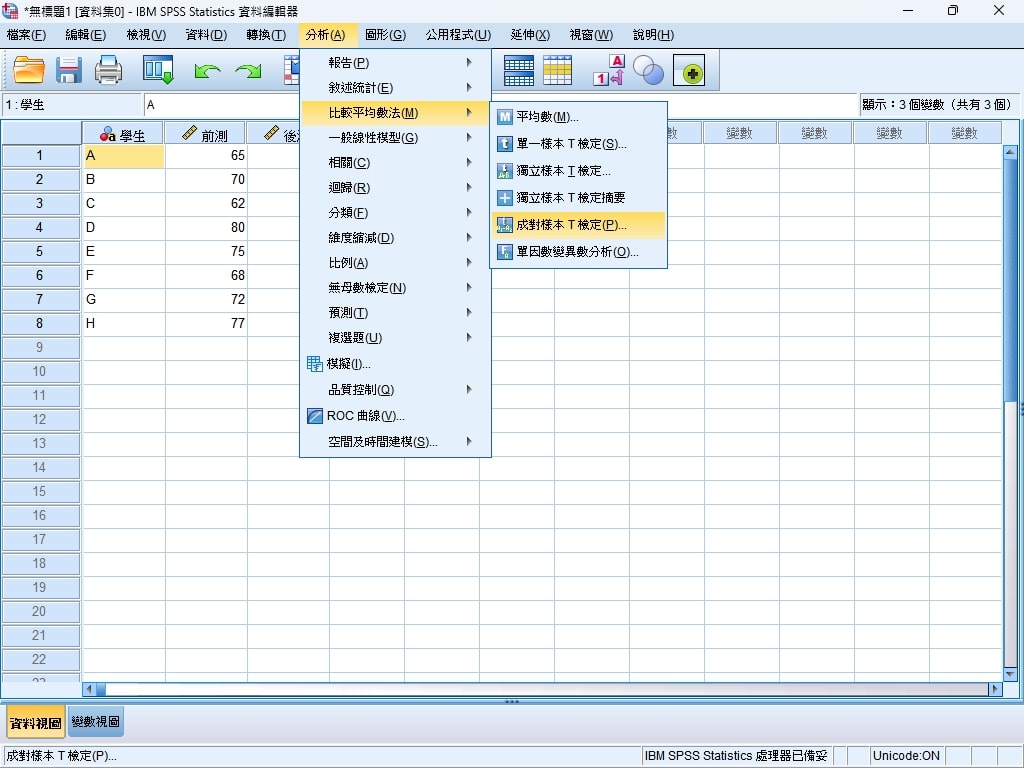
Step 4. 在後續彈出的設定視窗中，將前測拖曳至配對變數的變數1，將後測拖曳至配對變數的變數2，最後點選確定送出。

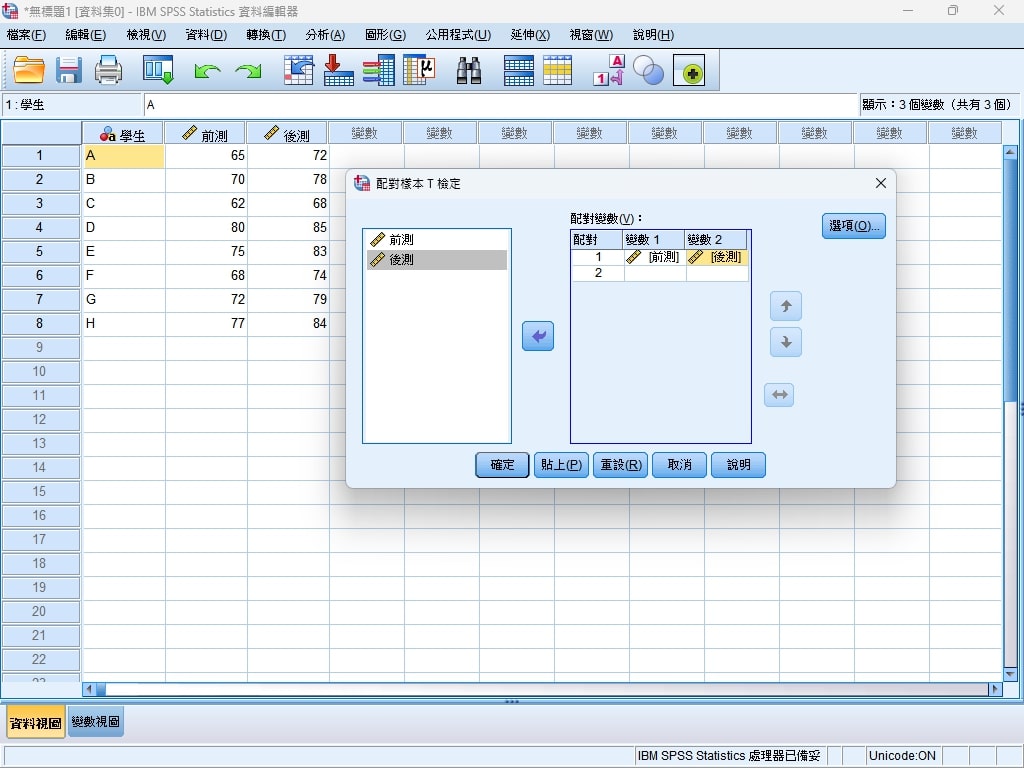
Step 5. 最後SPSS就會將統計分析後的數據報告呈現給我們看了。

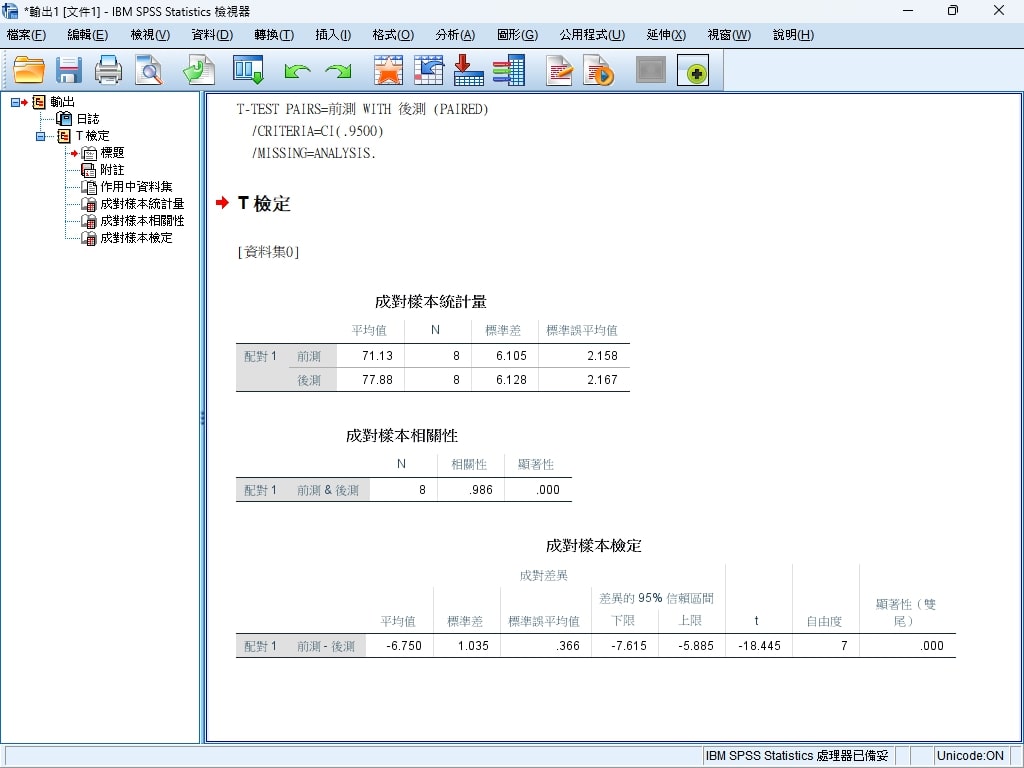
分析報告

以上面的例子，我們的獲取的分析報告資訊大致上如下：

1. 配對差異的描述

• 平均差異（Mean Difference）：-6.750 表示「後測」成績的平均值比「前測」高出6.75分。此負值表示後測成績普遍優於前測。

• 標準差（Standard Deviation）：1.035 表示各學生的前後測成績差異的分布情況。標準差較小，意味著大多數學生的成績提升幅度相近。

• 標準誤差（Standard Error of the Mean）：0.366 是平均差異的標準誤，表示樣本平均值的估計精度。標準誤越小，代表結果越穩定。

2. 95%信賴區間

• 信賴區間範圍為[-7.615, -5.885]，這意味著我們有95%的信心認為，真實的平均差異落在-7.615～-5.885之間。這區間不包含0故表示差異是顯著的。

3. T值和顯著性（p值）

• T值：-18.445 T值是一個統計量，代表差異的顯著性。T值越大（絕對值越高），代表差異越顯著。

• 自由度（df）：7 自由度為7，這裡的自由度是樣本數（8）減去1。

• 顯著性（雙尾p值）：.000 p值為0.000 小於 0.05，表示成對樣本之間的差異在統計上顯著。因此，可以拒絕虛無假設，說明ＯＯ教學方法對學生的微積分成績有顯著提升效果。

⭐總結 基於上述分析結果，顯示ＯＯ教學方法對學生的微積分成績有顯著的正向效果，且提升在統計上具顯著性（p < 0.05）。

相關連結：

• 統計：常態分佈、平均值、變異數與標準差
• 統計：一個簡單的樣本變異係數的運算範例
• 統計：一個簡單的幾何平均數的運算範例
• 統計：比較平均數法、T檢定、F檢定、p顯著性之說明
• 統計：獨立樣本T檢定之適用範圍與SPSS操作
• 統計：成對樣本T檢定之適用範圍與SPSS操作
• 統計：單因子變異數分析One-Way ANOVA之適用範圍與SPSS操作
• 統計：多因子變異數分析Two-Way ANOVA之適用範圍與SPSS操作
• 統計：皮爾森相關係數Pearson Correlation之適用範圍與SPSS操作
• 統計：線性迴歸Linear Regression之適用範圍與SPSS操作

SPSS Analysis Operation Flow StepByStep Paired Samples T-Test