三角函數sin(θ)的定義與簡單的應用

這篇文章記錄一下三角函數的正弦函數的簡單定義與生活上的計算應用。

甚麼是sin正弦函數

首先請看下圖，我們可以看到裡面有一個圓形，跟許多線條組成的三角形。

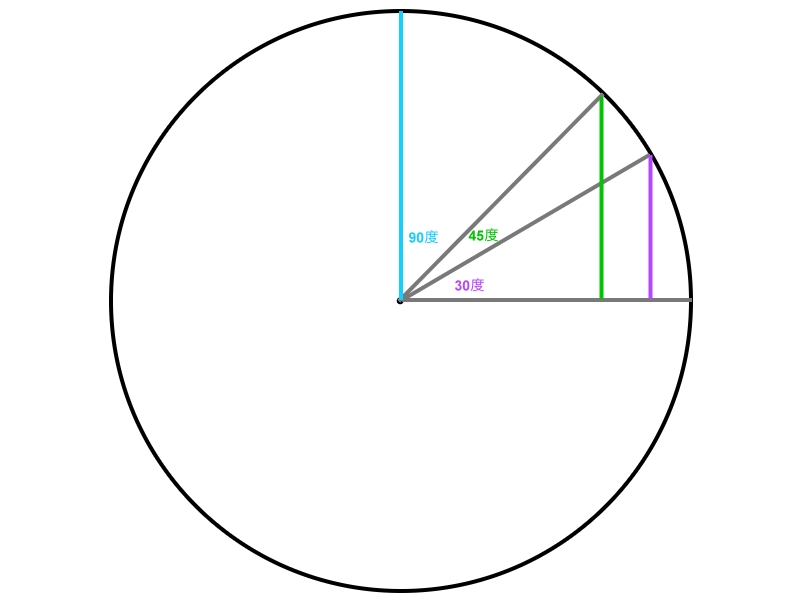
從上圖我們可以先將圓形中的灰色水平線定義成r，也就是圓形的半徑，這時候我們可以先將半徑的長度數值定義為1，半徑的單位是公分還是公尺不重要。

然後我們就可以開始推論sin(θ)了，sin(θ)其實就是半徑距離水平線（零度）的長度。

• θ角度： 0°，就相當於灰色線條所指出的地方，這時候根本沒有任何長度，因此sin(0)=0。
• θ角度：30°，就相當於紫色線條所指出的地方，這時候出現了一些距離長度了，sin(30)=0.5。
• θ角度：45°，就相當於綠色線條所指出的地方，這時候長度更加長了，sin(30)=0.7071。
• θ角度：90°，就相當於藍色線條所指出的地方，這時候長度達到最長，sin(90)=1。

小結

我們可以從上面的變化觀察出，其實sin(θ)的數值就是在0~1之間變化，變化的程度就是圓半徑的長短變化罷了。如果我們把0角度從0跑到359，然後紀錄每角度的sin(0)數值，連續紀錄並展開成時域，就可以得到經典的sin波形如下。

sin(θ)正弦函數的應用

假設你今天是一位工頭，站在一棟房屋的一樓地板看向二樓，想要在兩層樓地板之間做個樓梯，已知條件與圖形如下：

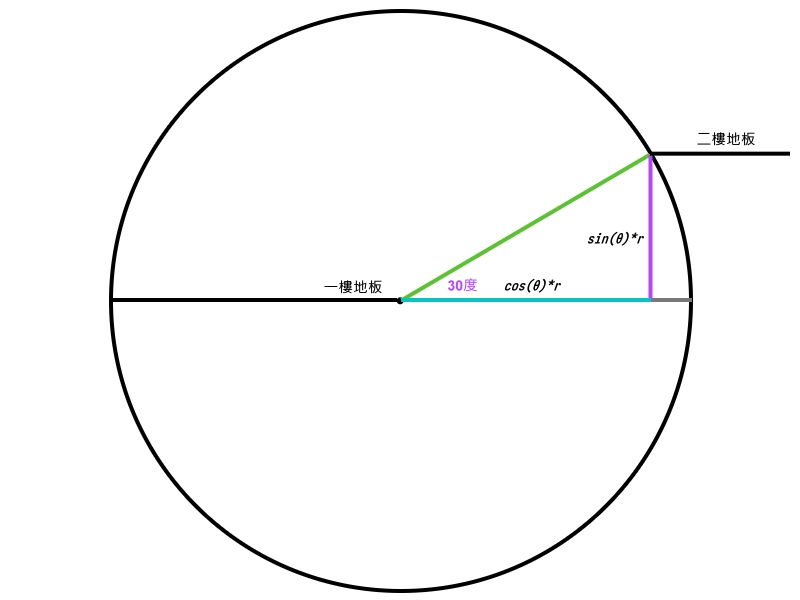
• 紫色線條：二樓到一樓的樓高為280公分。
• 紫色角度：一般樓梯的傾斜角度為30°比較安全。

試問：

1. 樓梯長度為幾公分？（綠色線條）
2. 站在一樓的你要怎麼估算樓梯的起點處？（藍色線條）

解答：

1. 樓梯長度為幾公分？（綠色線條）綠色線條計算的步驟如下：

sin(30) * r = 280
0.5 * r = 280
r = 280 / 0.5
r = 560

2. 站在一樓的你要怎麼估算樓梯的起點處？（藍色線條）

藍色線條表示的其實就是cos(θ)餘弦函數，他的數值剛好跟sin(θ)相差90°，也就是當

• θ角度： 0°，cos(0)=1，就是等於圓半徑長度。
• θ角度：90°，cos(90)=0。

因此計算步驟如下：

//由上面求得樓梯長度（也就是圓半徑r）為560
cos(30) * 560 = 484.974226

由上面這個數值可以知道，工頭只要從二樓吊一個鉛錘線下來到一樓，取得一點之後，再從此點計算484.974226公分，就是樓梯的終點位置。

驗算

依據畢氏定理，假設a、b、c為△ABC的三邊。若∠C=90°, 則A² + B² = C²。

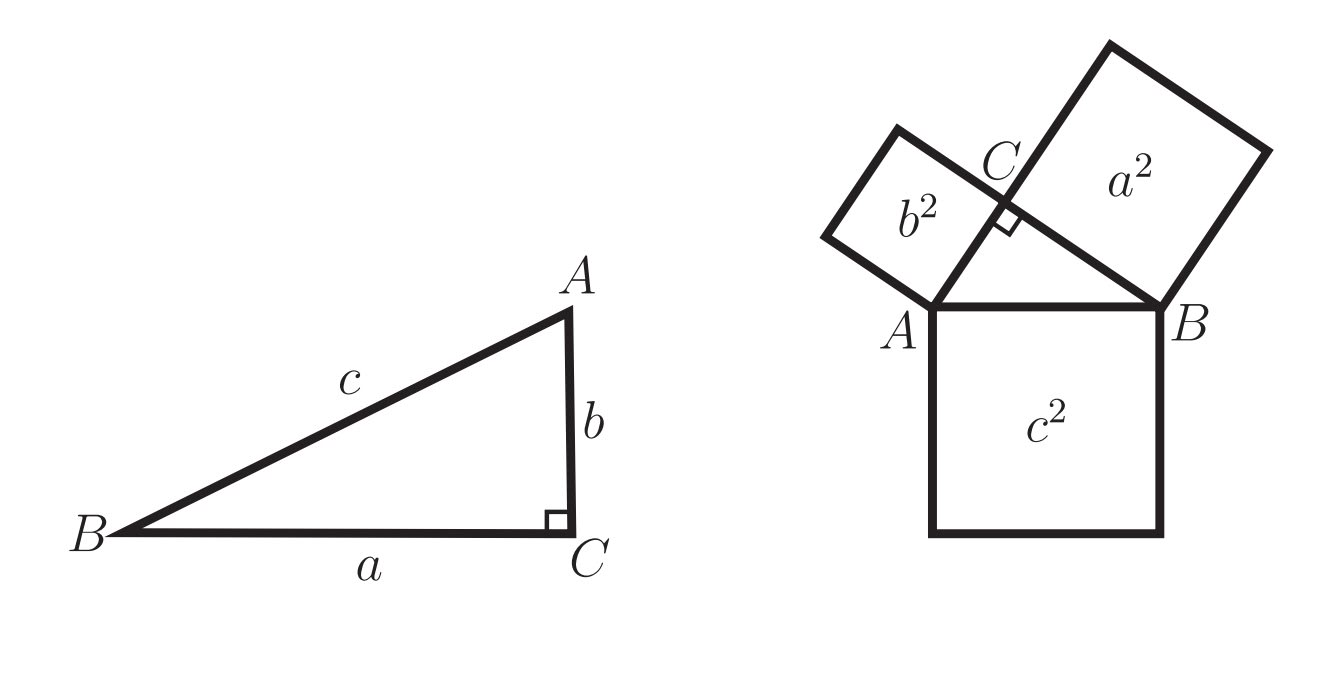
因此把上面的計算結果取出驗證A² + B²：

(484.974226)² + (280)² = 235,199.999884299076 + 78400
= 313,599.999884

而C²為：

(560)² = 313600

313,599.999884趨近於≈313600，因此證明整個三角函數的計算過程是正確的。

後記補充

如果你有仔細地了解後，會發現角度套入(cos(θ), sin(θ))，其實就是圓周的座標(x, y)，大學時期曾經利用這個小運算來移動滑鼠座標來表示某系統的待機狀態。

三角函數 正弦函數 餘弦函數 sin(θ) cos(θ) 生活應用 計算