統計：一個簡單的幾何平均數的運算範例
幾何平均數相較於生活中最常用到的算術平均數（Arithmetic Average）而言，來的比較難計算（以人類徒手計算的觀點），但是在某些情況下，卻更能夠抵抗雜訊（突波）的干擾，更真實的反映出人類期望看到的狀態。
舉例來說，想要依照收入來換算平均一個國家的人民的幸福指數，假設這個國家的中產階級（鐘型曲線中間）年收入約為80萬，可能在尾端年收入10萬的人，其心目中感到的幸福指數，不見得一定是中產階級的0.125倍而已。同樣的道理，可能這個國家的頂級富豪年收入是1億，其心中的幸福指數，也不可能是中產階級的125倍。這鐘型曲線的兩端，都是屬於統計上面的雜訊，透過幾何平均計算，我們可以將平均值取得「較不為那麼敏感」。
簡單的說，如果有一個數列接近自然分布，那麼幾何平均數的意義會更具有參考價值。幾何平均數的公式如下所示：
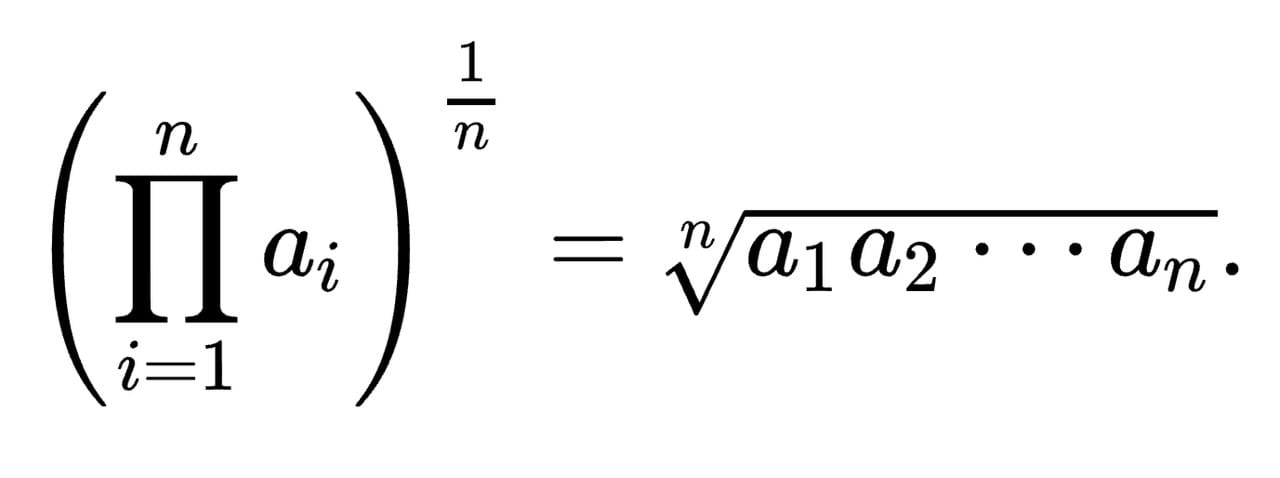
幾何平均數（Geometric mean）的「單純數列」計算範例
假設有一個數列為「1、4、5、6、7、3、8、4、9」，那麼其算術平均數（X̄）為：5.2，其幾何平均數的計算過程如下所示：
1 x 4 x 5 x 6 x 7 x 3 x 8 x 4 x 9 = 725760
725760 ^ (1/9) = 4.4791（GM）
幾何平均數（Geometric mean）的「定存年利率」計算範例
假設有一個銀行，其定存利率的變化過程為：1.5%維持2.3年、2.1%維持1.2年、1.8%維持0.8年、1.75%維持1.5年，其幾何平均年利率為：
(1.015 ^ 2.3) X (1.021 ^ 1.2) X (1.018 ^ 0.8) X (1.0175 ^ 1.5) = 1.1046
(1.1046 ^ (1/(2.3 + 1.2 + 0.8 + 1.5))) - 1 = 1.73%（GM）
幾何平均數（Geometric mean）的「年化報酬率」計算範例
年化報酬率（Annualized Rate of Return）一直是投資理財的重點計算方法，而幾何平均數在這邊被利用的有點巧妙，有經過前面幾個範例的介紹，應該都可以看出一點，就是幾何平均不適用「負值」，因為在相乘運算過程的正負之間會影響到結果的判讀。然而哪個投資不會虧損？總會有幾年的報酬率是負數的吧？因此我們會透過先統一＋１，之後結果再去統一減去１的技巧，來將負值的詭異點破除。
小明去年五年之間，每一個年度的投資報酬如下：
第一年 10%
第二年 8%
第三年 -12%（大虧）
第四年 5%
第五年 7%
計算小明這五年的年化報酬率為：
//先統一將每年的報酬率加一消除負獲利，再將其相乘。
1.1 X 1.08 X 0.88 X 1.05 X 1.07 = 1.1745
1.1745 ^ (1/5) = 1.0327
//將計算出來的幾何平均值減去一，回歸正常
1.032 - 1 = 3.27%
所以小明的年化報酬率是3.27%喔，看起來也是還好而已嘛！:P
相關連結：
20211018修正
感謝網友phi來信針對「定存年利率」勘誤，敝人將1.8%在計算過程中誤植導致計算錯誤，網頁內文已經修正，再次感謝phi網友的熱心協助。