統計：一個簡單的樣本變異係數的運算範例

今日有用到統計學上面的變異係數（CV；Coefficient of Variation）的計算，將計算過程羅列在這邊，供給日後有需要的網友參考一下。

題目：請試算（1、2、5、6）四個數值的變異係數。

要進行變異係數的計算，首先我們必須要準備兩個參數，一個是樣本平均數（X̄）、一個是樣本標準差（s），公式分別為下圖所示。

樣本平均數（X̄）

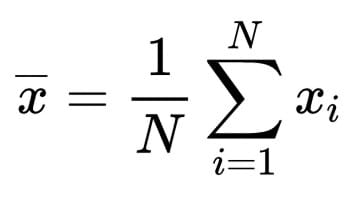
計算樣本平均數（X̄）

1 + 2 + 5 + 6 = 14
14 / 4 = 3.5 = X̄

樣本標準差（s）

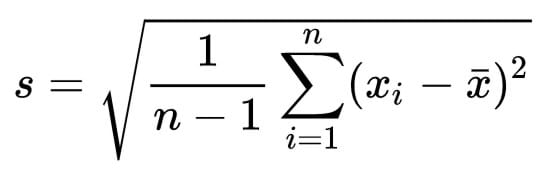
計算樣本標準差（s）

√(1/4-1)((1-3.5)^2 + (2-3.5)^2 + (5-3.5)^2 + (6-3.5)^2)
√(1/4-1)(6.25 + 2.25 + 2.25 + 6.25)
√(1/3)(17)
√5.666 = 2.38 = s

有了平均數（X̄）跟樣本標準差（s），就可以計算出變異係數(CV；Coefficient of Variation)。

CV = s / X̄ = 2.38 / 3.5 = 0.68

因此樣本（1、2、5、6）的變異係數是0.68。